Examples#

Almost homoskedastic noise#

In this example we apply the Dyson Equalizer on data with Gaussian almost homoskedastic noise.

The signal X consists of 10 strong and 10 weak components to which Gaussian noise was added to create the data matrix Y = X + E. The noise E was homoskedastic everywhere with the exception of 5 rows and 5 columns, which have abnormally strong noise.

Initializing the DysonEqualizer class with the data class Y and calling compute()
Calling the plot_mp_eigenvalues_and_densities function. The option show_only_significant=1 was specified to limit the x-axis to the first non-noise eigenvalue, since the larges signal eigenvalues are large.

import matplotlib.pyplot as plt
import numpy as np
from dyson_equalizer.dyson_equalizer import DysonEqualizer
from dyson_equalizer.examples import generate_Y_with_almost_homoskedastic_noise

Y = generate_Y_with_almost_homoskedastic_noise()
de = DysonEqualizer(Y).compute()
de.plot_mp_eigenvalues_and_densities(show_only_significant=1)

(Source code, png, hires.png, pdf)

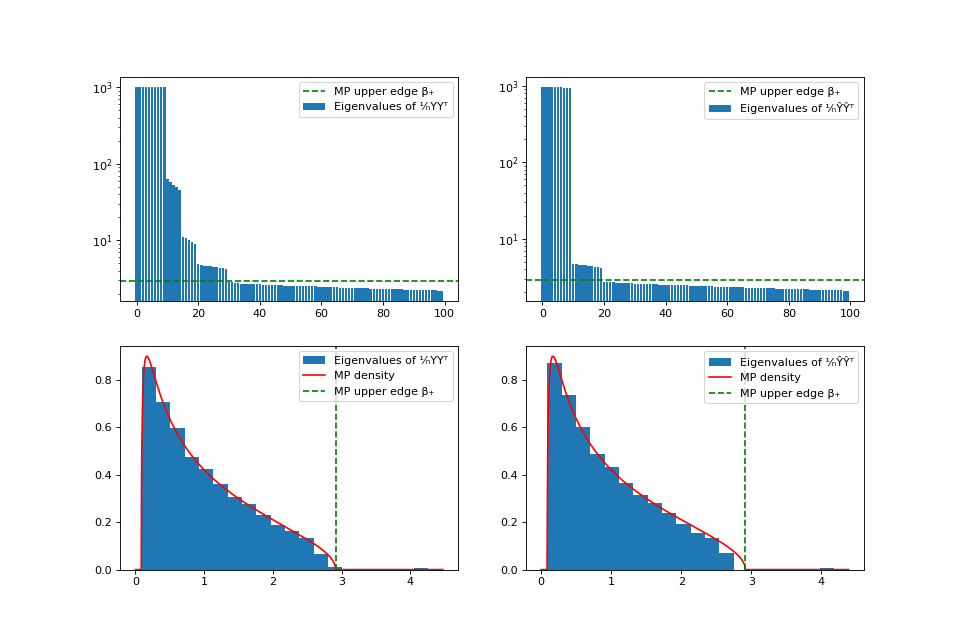
_images/examples-1.png — Spectrum of the data before (left) and after (right) applying the normalization of Dyson Equalizer.#

We observe that the eigenvalue spectrum of the normalized ¹⁄ₙŶŶᵀ matrix follows the theoretical Marchenko-Pastur (MP) distribution and that the MP upper edge β₊ correctly matches the rank of the signal. On the other hand, the eigenvalue spectrum of ¹⁄ₙYYᵀ contains extra eigenvalues due to the abnormal noise and the threshold β₊ would identify more than 20 significant components.

Heteroskedastic noise#

In this example we apply the Dyson Equalizer on data with Gaussian heteroskedastic noise. The signal X consists of 10 strong and 10 weak components to which Gaussian heteroskedastic noise was added to create the data matrix Y.

Next, we compute the Dyson Equalizer and plot the eigenvalues distributions by

Initializing the DysonEqualizer class with the data class Y and calling compute()
Calling the plot_mp_eigenvalues_and_densities function. The option show_only_significant=1 was specified to limit the x-axis to the first non-noise eigenvalue, since the larges signal eigenvalues are large.

import matplotlib.pyplot as plt
import numpy as np
from dyson_equalizer.dyson_equalizer import DysonEqualizer
from dyson_equalizer.examples import generate_Y_with_heteroskedastic_noise

Y = generate_Y_with_heteroskedastic_noise()
de = DysonEqualizer(Y).compute()
de.plot_mp_eigenvalues_and_densities(show_only_significant=1)

(Source code, png, hires.png, pdf)

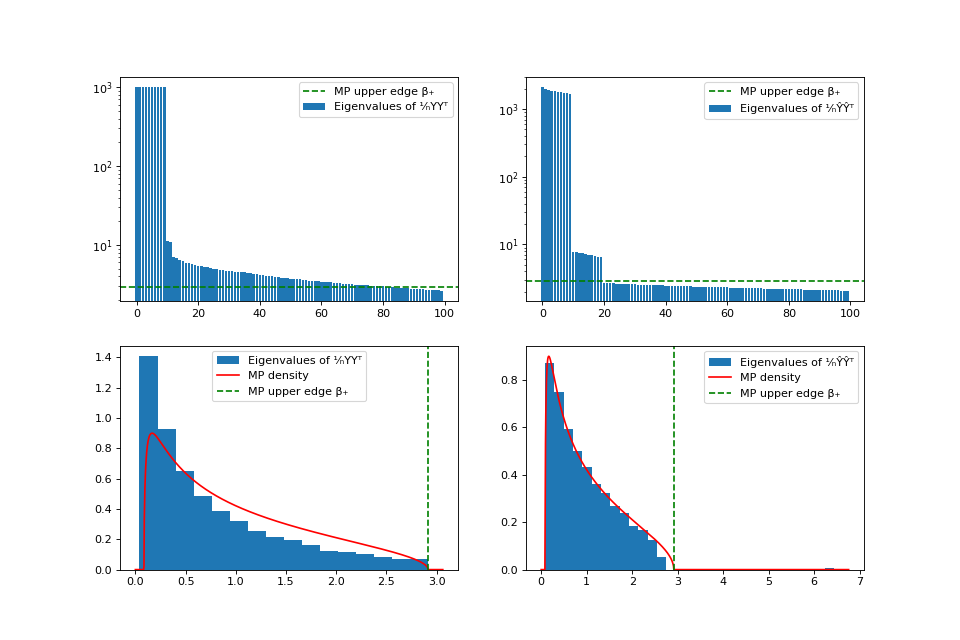
_images/examples-2.png — Spectrum of the data before (left) and after (right) applying the normalization of Dyson Equalizer.#